| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Figure it Out (Page 219) | Figure it Out (Page 223 - 230) | Figure it Out (Page 235 - 236) |
| Figure it Out (Page 238) | ||
Chapter 9 Symmetry
Welcome to the solutions guide for Chapter 9, "Symmetry," a fascinating exploration within the Class 6 Ganita Prakash mathematics textbook, published by NCERT for the 2024-25 academic session. This chapter invites students into the visually appealing world of balance, harmony, and geometric regularity. Symmetry is a fundamental concept found not only in mathematics but also extensively in nature, art, architecture, and design. These solutions are meticulously prepared to help students grasp the core ideas of symmetry, primarily focusing on reflectional symmetry, more commonly known as line symmetry, and to provide clear, step-by-step methods for solving the exercises presented.
The central theme of this chapter revolves around understanding what makes a shape symmetrical. The solutions provide detailed explanations and numerous illustrations focusing on line symmetry. A figure possesses line symmetry if it can be divided by a line – the line of symmetry or axis of symmetry – into two identical halves that are mirror images of each other. Imagine folding the figure along this line; the two parts would perfectly coincide, overlapping exactly. The solutions demonstrate how to identify these crucial lines in a variety of contexts. Students will find clear answers showing the lines of symmetry for:
- Geometric Shapes: Including triangles (distinguishing between an equilateral triangle with 3 lines of symmetry, an isosceles triangle with 1 line, and a scalene triangle with 0 lines), various quadrilaterals (like a square with 4 lines, a rectangle with 2 lines, a rhombus with 2 lines, but a general parallelogram with none), and the special case of a circle, which possesses an infinite number of lines of symmetry passing through its center.
- Letters of the English Alphabet: Examining letters like 'H' (2 lines), 'A' (1 vertical line), 'B' (1 horizontal line), 'O' (multiple/infinite lines ideally, often treated as 2), versus letters like 'F', 'G', or 'P' which have no lines of symmetry.
A key practical skill developed in this chapter, and thoroughly addressed in the solutions, is the ability to complete a figure when given only half of it along with the line of symmetry. The solutions provide detailed instructions and visual guides demonstrating how to accurately reflect the given portion across the line of symmetry to construct the whole, symmetrical shape. This reinforces the mirror-image concept fundamental to reflectional symmetry. While the primary focus remains on line symmetry, some solutions might briefly touch upon the related concept of rotational symmetry. This involves identifying if a shape can be rotated around a central point (the center of rotation) by less than a full $360^\circ$ turn and still look exactly the same. The number of times it matches itself during one full rotation defines its order of rotational symmetry (e.g., a square has rotational symmetry of order 4).
By engaging with these carefully constructed solutions for Chapter 9 of the Class 6 Ganita Prakash (NCERT 2024-25), students are expected to significantly enhance their visual perception and spatial reasoning skills. They learn to recognize and appreciate symmetrical patterns, understand the precise geometric definition of line symmetry, and apply this understanding methodically to analyze both familiar shapes and abstract figures. This chapter builds an intuitive yet formal understanding of a concept that resonates throughout geometry and beyond.
Figure it Out (Page 219)




Question 1. Do you see any line of symmetry in the figures at the start of the chapter? What about in the picture of the cloud?
Answer:
Let's examine the figures provided at the start of the chapter.
Looking at the images, particularly the first image (27.jpg) and the figures in the other images (1.jpg, 2.jpg, 3.jpg), many of them appear to have lines of symmetry.
For example:
The first image (27.jpg) shows a design that appears to have multiple lines of symmetry passing through its center.
Image 1.jpg shows a butterfly, which typically has a vertical line of symmetry down its body.
Image 3.jpg shows a leaf, which also often has a line of symmetry along its central vein.
Image 2.jpg shows a design that has rotational symmetry, but it might also have lines of symmetry depending on the exact pattern.
So, yes, we can see lines of symmetry in many of the figures shown at the start of the chapter.
Now let's consider the picture of the cloud.
A cloud is a natural formation with an irregular and constantly changing shape. While some idealized drawings or simple representations of clouds might be drawn with symmetry, a real picture of a cloud, as it appears in nature, generally does not have a definite line of symmetry.
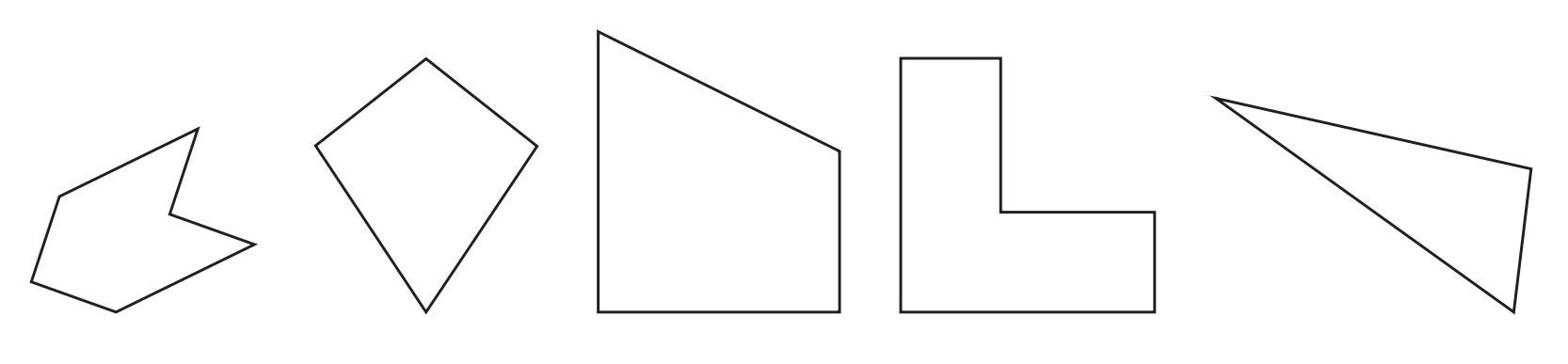
Answer:
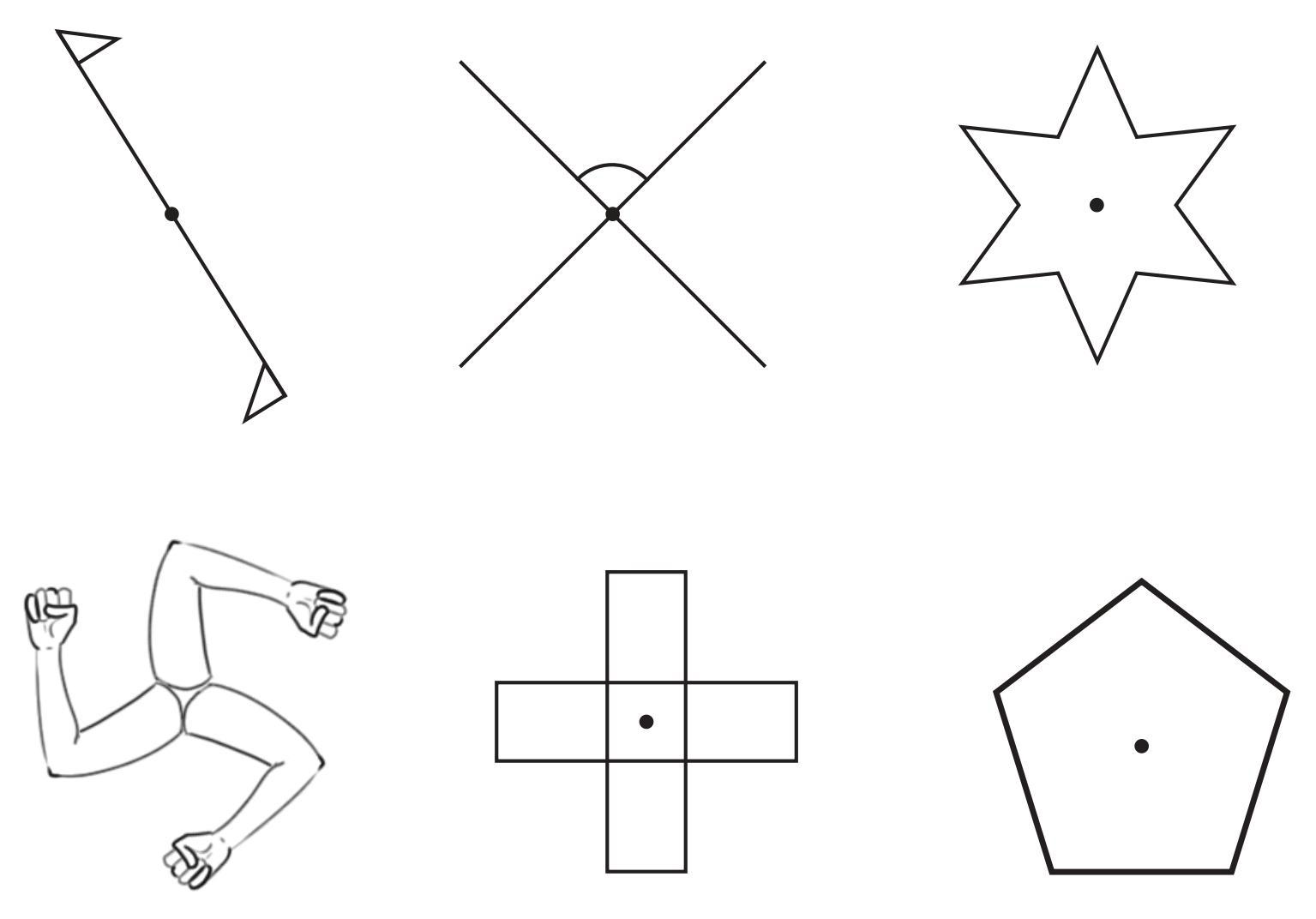
Let's examine each figure in the provided image to identify its line(s) of symmetry.
Figure 1 (Hourglass shape):
This figure has two lines of symmetry.
One is a horizontal line passing through the narrowest part of the figure, dividing it into identical top and bottom halves.
The other is a vertical line passing through the center of the figure, dividing it into identical left and right halves.
Figure 2 (Arrow pointing up):
This figure has one line of symmetry.
It is a vertical line passing through the tip of the arrow and the midpoint of its base, dividing the figure into identical left and right halves.
Figure 3 (Star shape):
This figure has one line of symmetry that is easily identifiable from the drawing.
It is a vertical line passing through the top point of the star, dividing it into identical left and right halves (assuming the star is drawn symmetrically).
Note: If it were a regular 5-pointed star, it would have 5 lines of symmetry.
Figure 4 (Letter H):
This figure has two lines of symmetry.
One is a vertical line passing through the middle of the crossbar and the centers of the top and bottom horizontal lines, dividing the figure into identical left and right halves.
The other is a horizontal line passing through the middle of the vertical lines and the crossbar, dividing the figure into identical top and bottom halves.
Figure 5 (Letter A):
This figure has one line of symmetry (assuming it is drawn symmetrically).
It is a vertical line passing through the peak of the letter and the midpoint of its base, dividing the figure into identical left and right halves.
Figure it Out (Page 223 - 230)
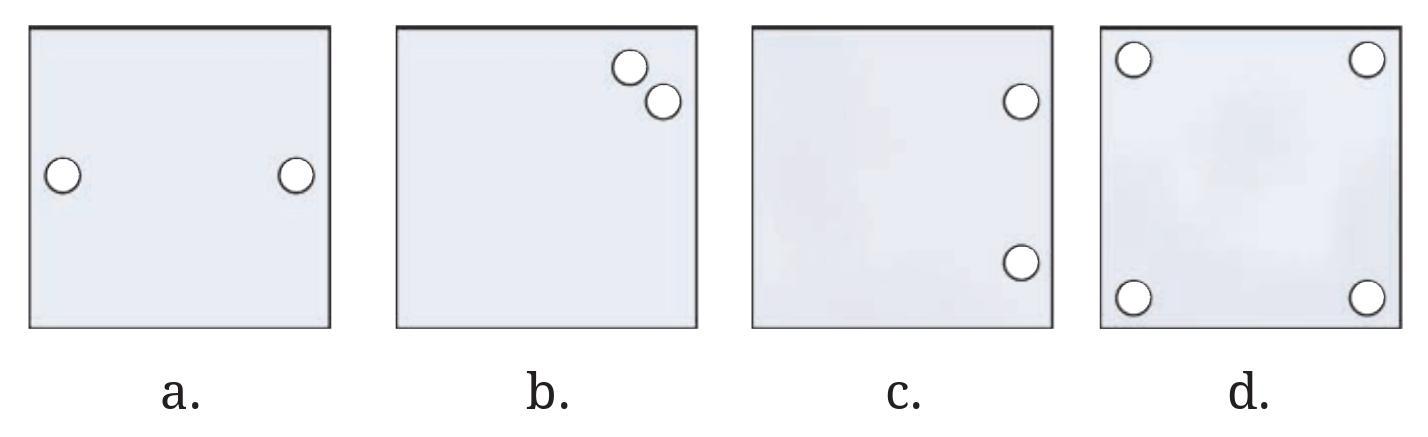
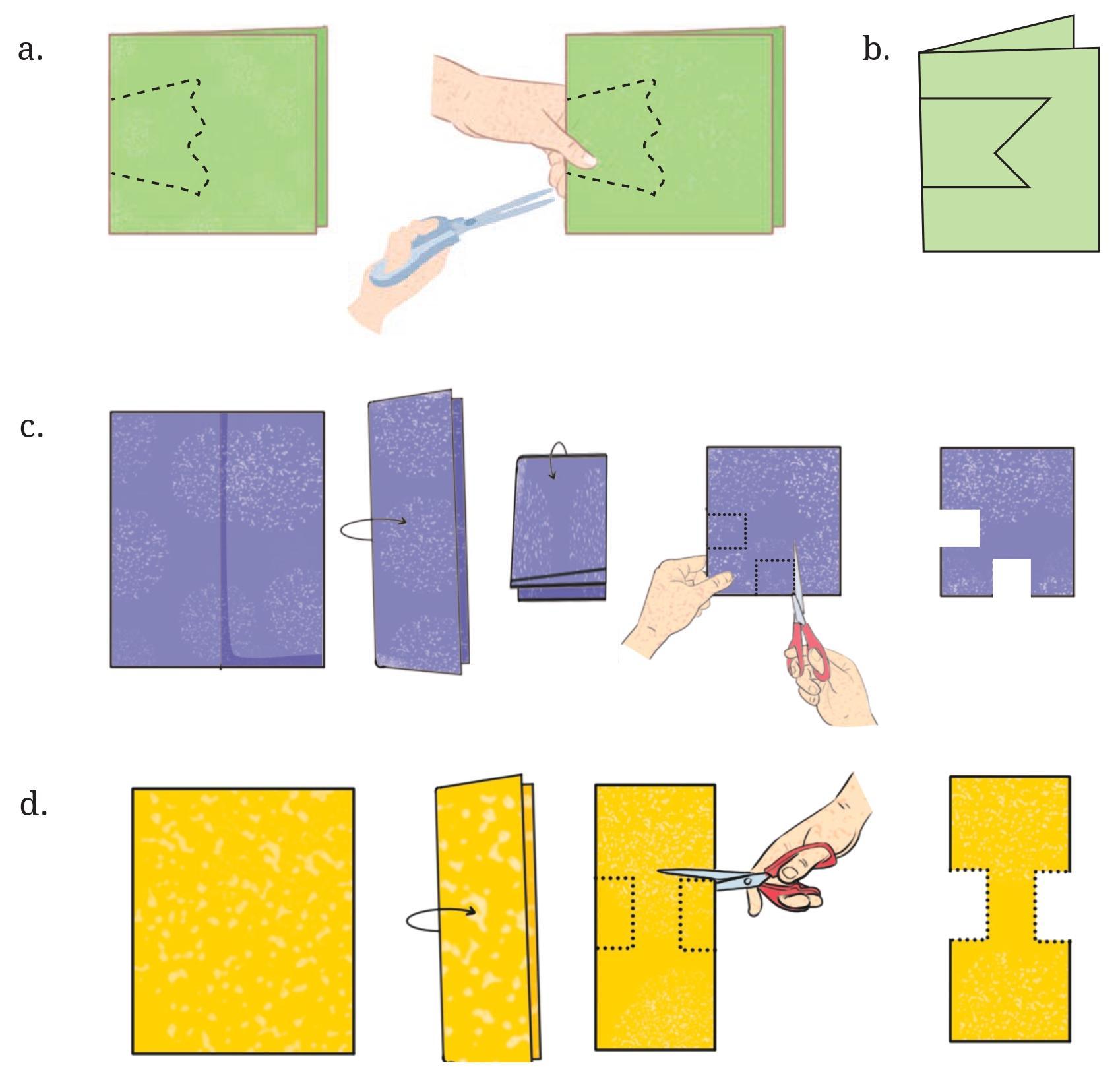
Figure (d) was created by punching a single hole. How was the paper folded?
Answer:
In each figure, the holes are located such that they are reflections of each other across the fold line. The fold line is the line of symmetry that relates the position of the original hole (or holes) to its reflection(s).
Identifying the Fold Line:
For each figure, the fold line is the line of symmetry for the pattern of holes.
Figure (a): There are two holes, horizontally aligned. The fold line is the vertical line exactly midway between the two holes.
Figure (b): There are four holes, symmetrically arranged. The fold line is the horizontal line passing through the center of the square, midway between the top two and bottom two holes.
Figure (c): There are two holes, vertically aligned. The fold line is the horizontal line exactly midway between the two holes.
Figure (d): There are two holes, diagonally placed relative to the square. The fold line is the diagonal line of the square passing through the center, such that one hole is the reflection of the other across this diagonal. There are two possible diagonal fold lines for a square. The correct one is the one that passes symmetrically between the two holes.
How Figure (d) was folded:
Figure (d) was created by punching a single hole. Since the unfolded paper shows two holes, this means the paper was folded once such that when the hole was punched, it went through both layers of the folded paper. The resulting two holes are mirror images of each other across the fold line.
To get the pattern in Figure (d) with a single punch, the paper must have been folded along one of its diagonals.
The steps for folding would be:
1. Take a square sheet of paper.
2. Fold the paper along one of its diagonals. For example, fold the bottom-left corner onto the top-right corner, or the bottom-right corner onto the top-left corner.
3. While the paper is folded along the diagonal, punch a single hole through both layers of the paper at the desired location (which corresponds to one of the holes shown in Figure (d)). The punch should not be on the fold line itself, nor should it be in the corner where the edges meet.
4. Unfold the paper. You will see two holes, symmetrically placed with respect to the diagonal fold line.

Answer:
When a paper is folded along a line and a hole is punched, the hole appears in every layer that was under the punch. When unfolded, the pattern of holes is symmetric with respect to the fold line(s). The other holes are the reflections of the given hole(s) across the line(s) of symmetry.
Figure (a):
Given is one hole and a vertical line of symmetry.
The other hole will be the reflection of the given hole across the vertical line.
It will appear horizontally opposite to the given hole, at the same distance from the vertical line.
Figure (b):
Given are two holes and a horizontal line of symmetry.
The other holes will be the reflections of the given two holes across the horizontal line.
For each given hole, its reflection will appear vertically opposite to it, at the same distance from the horizontal line.
This will result in a total of four holes, forming a symmetrical pattern about the horizontal line.
Figure (c):
Given is one hole and a diagonal line of symmetry.
The other hole will be the reflection of the given hole across the diagonal line.
Imagine folding the paper along the diagonal; the other hole appears at the corresponding position on the other side of the diagonal.
Figure (d):
Given are two holes and two lines of symmetry (vertical and horizontal) passing through the center.
The complete pattern must be symmetrical with respect to both the vertical and horizontal lines.
The given two holes are already symmetrical about the horizontal line.
Reflecting these two holes across the vertical line will produce two more holes.
The two given holes are in the bottom half. Reflecting them across the vertical line will produce two holes in the bottom half, mirroring the originals horizontally.
The final pattern will have four holes, arranged symmetrically around the center.
Figure (e):
Given is one hole and a vertical line of symmetry.
The other hole will be the reflection of the given hole across the vertical line.
It will appear horizontally opposite to the given hole, at the same distance from the vertical line.
Figure (f):
Given is one hole and two lines of symmetry (vertical and horizontal) passing through the center.
The complete pattern must be symmetrical with respect to both the vertical and horizontal lines.
Reflecting the given hole across the vertical line produces a second hole.
Reflecting the original hole across the horizontal line produces a third hole.
Reflecting the second hole (or the third hole) across the remaining symmetry line produces a fourth hole.
The final pattern will have four holes, symmetrically placed in all four quadrants relative to the center.
Consider a vertical fold. We represent it this way:
Similarly, a horizontal fold is represented as follows:
Answer:
The question asks about the result of a sequence of paper folds and a cut. We are shown a square paper, a sequence of three folds, and a cut made on the final folded shape. We are also introduced to notations for vertical and horizontal folds.
Sequence of Folds:
Based on the image (7.jpg) and the notation examples (8.jpg), the sequence of folds is as follows:
1. First Fold: A vertical fold. The square is folded in half along the vertical bisector. The right half is folded onto the left half. This introduces a vertical line of symmetry.
2. Second Fold: A horizontal fold. The paper (now folded in half) is folded again in half along the horizontal bisector. The bottom half is folded onto the top half. This introduces a horizontal line of symmetry. After these two folds, the paper is folded into a smaller square, which is $1/4$ the area of the original square, and consists of $4$ layers of paper.
3. Third Fold: A diagonal fold. The resulting small square is folded diagonally. Observing the image, it appears that one corner (the bottom-left corner of the twice-folded square) is folded upwards onto the opposite edge (the top edge of the twice-folded square). The fold line is a diagonal segment starting from the bottom-right corner (which corresponds to the center of the original square) and extending upwards to the top edge.
The final shape after these three folds is a triangle.
The Cut:
A cut is made on the final folded triangular shape. The image shows the cut as a concave arc made along the longest edge (the hypotenuse) of the triangle, cutting inwards from that edge.
Unfolding and Symmetry:
When the paper is unfolded, the cut shape is revealed. Each fold line acts as a line of symmetry. The shape of the cut is reflected across each fold line during the unfolding process.
1. Unfolding the third (diagonal) fold: The concave arc cut is reflected across the diagonal fold line. Since the cut was made on the edge which is the diagonal fold line, this reflection will create a shape bounded by two concave arcs meeting at the endpoints of the original cut. This shape lies symmetrically across the diagonal fold line.
2. Unfolding the second (horizontal) fold: The shape created after the first unfolding step is reflected across the horizontal bisector of the original square. This reproduces the pattern in the bottom half of the paper.
3. Unfolding the first (vertical) fold: The pattern obtained after the second unfolding step is reflected across the vertical bisector of the original square. This reproduces the pattern in the right half of the paper.
The combination of these reflections due to the symmetries introduced by the folds results in a final pattern in the unfolded square.
Resulting Shape:
The specific sequence of folds (Vertical, Horizontal, Diagonal) combined with a concave arc cut on the hypotenuse edge results in a symmetrical pattern. Based on common paper cutting problems and the nature of the cut, this process yields a four-pointed star when the paper is completely unfolded.
Answer:
We need to predict the shape of the hole created when the folded and cut paper is unfolded. The process of unfolding is the reverse of folding, and the resulting shape will have symmetry with respect to the fold line(s).
Analysis of Figure (a):
1. The square paper is folded vertically in half.
2. The paper (now a rectangle) is folded horizontally in half. The paper is now a smaller square, $1/4$ the size of the original, with $4$ layers.
3. A semicircular cut is made on one of the edges of the small square. This edge corresponds to the vertical bisector of the original square.
Prediction: When unfolded across the horizontal fold line, the semicircle is reflected, forming a full circle. When unfolded across the vertical fold line, this circle (which is centered on the vertical line if the semicircle was centered on the edge) is reflected onto itself. Thus, a single circle will be formed in the center of the square.
Analysis of Figure (b):
1. The square paper is folded vertically in half.
2. The paper is folded horizontally in half. The paper is now a smaller square with $4$ layers.
3. A triangular cut is made on one of the edges of the small square. This edge corresponds to the vertical bisector of the original square.
Prediction: When unfolded across the horizontal fold line, the triangular cut is reflected, forming a rhombus (diamond shape) with the base of the triangle forming one diagonal of the rhombus. When unfolded across the vertical fold line, this rhombus (which is centered on the vertical line if the triangle's base was centered on the edge) is reflected onto itself. Thus, a single rhombus (diamond shape) will be formed in the center of the square.
Analysis of Figure (c):
1. The square paper is folded diagonally in half. The paper is now a right-angled triangle with $2$ layers.
2. The resulting triangle is folded again. Based on the image, the right-angle vertex is folded onto the hypotenuse (the original diagonal). The fold line is a segment of the other diagonal of the original square, passing through the center. The paper is now a smaller triangle with $4$ layers.
3. A triangular cut is made on the edge which corresponds to the original diagonal fold line (the hypotenuse of the first folded triangle).
Prediction: When unfolded across the second fold line (the segment of the other diagonal), the triangular cut made on the edge (the first diagonal) is reflected. This will create a shape symmetric about the second diagonal segment, lying on the first diagonal. When unfolded across the first fold line (the main diagonal), the shape formed on the diagonal is revealed. Due to the symmetries introduced by this common folding sequence (diagonal, then along altitude), a triangular cut made near the center of the edge corresponding to the diagonal often results in an 8-pointed star-like hole centered in the square.
To verify these predictions, you would need to perform the actual paper folding and cutting steps as described for each figure.
Question 5. Suppose you have to get each of these shapes with some folds and a single straight cut. How will you do it?
a. The hole in the centre is a square.

b. The hole in the centre is a square.

Note: For the above two questions, check if the 4-sided figures in the centre satisfy both the properties of a square.
Answer:
To get a square hole in the centre of a shape using folds and a single straight cut, we need to fold the paper in a specific way that the four sides of the intended square hole are aligned along a single line or are created by symmetry when a single cut is made.
Method to obtain a square hole:
1. Start with a rectangular or square piece of paper.
2. Fold the paper in half along its length.
3. Fold the resulting shape in half along its width. The intersection of the two creases marks the exact centre of the paper, which will be the centre of the square hole.
4. Fold one of the corners formed by the previous folds (the corner representing the centre of the original paper) downwards. Make sure the tip of this corner lies precisely on the opposite folded edge. This fold line will pass through the centre point and create a $45^\circ$ angle with the edges of the quarter-folded paper.
5. Fold the adjacent edge of this quarter-folded paper onto the fold line created in the previous step. This aligns several layers of paper along the line where the single straight cut will be made.
6. Make a single straight cut across the folded layers of paper. This cut should be perpendicular to the aligned folded edges and should be made at a distance from the pointed corner (the centre) corresponding to the desired size of the square hole.
7. Carefully unfold the paper. A square hole will be revealed in the centre.
Verification of the shape of the hole:
The properties of a square are:
i) All four sides are of equal length.
ii) All four interior angles are right angles ($90^\circ$).
The folding process described above utilizes symmetry. The initial folds establish perpendicular axes of symmetry. The subsequent folds and the single straight cut, made perpendicular to the aligned edges formed by the folds originating from the centre, ensure that when the paper is unfolded, the cut segment is replicated symmetrically to form a four-sided figure with equal sides and $90^\circ$ angles.
Therefore, the 4-sided figure in the centre obtained by this method satisfies both properties of a square. The hole in the centre is indeed a square.
Application to Figures (a) and (b):
The method described above is the fundamental technique used to create a square hole in a piece of paper with folds and a single straight cut. This method applies to creating the square holes shown in both figures (a) and (b).
The specific outer shape of the paper in figures (a) and (b) depends on the initial shape of the paper used and the exact location and length of the single straight cut relative to the edges of the paper and the folds. In some cases, the single cut might define segments of both the inner square hole and the outer boundary simultaneously.
Regardless of the resulting outer shape, the inner hole created by the described folding and cutting process will be a square, satisfying both the condition of having equal sides and the condition of having right angles, as verified above.
i.
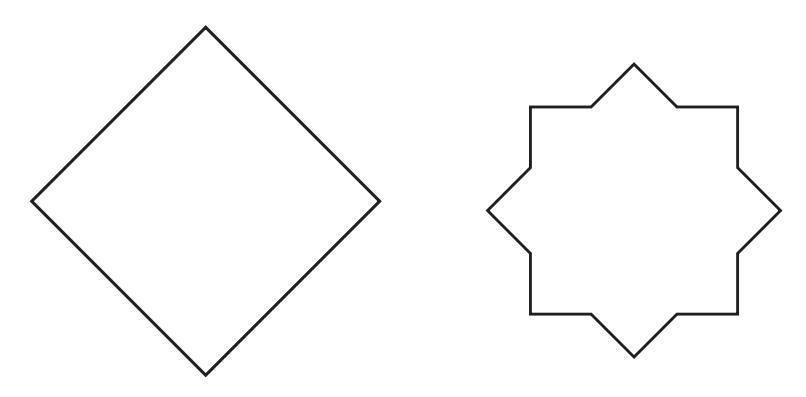
ii. A triangle with equal sides and equal angles.
iii. A hexagon with equal sides and equal angles.
Answer:
For each shape, we identify the type and then state the number of lines of symmetry.
i. The given shape is a rectangle with a concentric square hole.
A rectangle has 2 lines of symmetry, passing through the midpoints of opposite sides. A square has 4 lines of symmetry, passing through the midpoints of opposite sides and along the diagonals. When a square hole is placed concentrically within a rectangle, the lines of symmetry for the combined shape are the lines that are common to both the outer rectangle and the inner square and pass through their common center. These are the lines passing through the midpoints of the opposite sides.
Therefore, the shape has 2 lines of symmetry.
ii. A triangle with equal sides and equal angles is an equilateral triangle.
An equilateral triangle has 3 lines of symmetry. These lines pass through each vertex and the midpoint of the opposite side.
Therefore, the shape has 3 lines of symmetry.
iii. A hexagon with equal sides and equal angles is a regular hexagon.
A regular hexagon has 6 lines of symmetry. These lines pass through opposite vertices (3 lines) and through the midpoints of opposite sides (3 lines).
Therefore, the shape has 6 lines of symmetry.
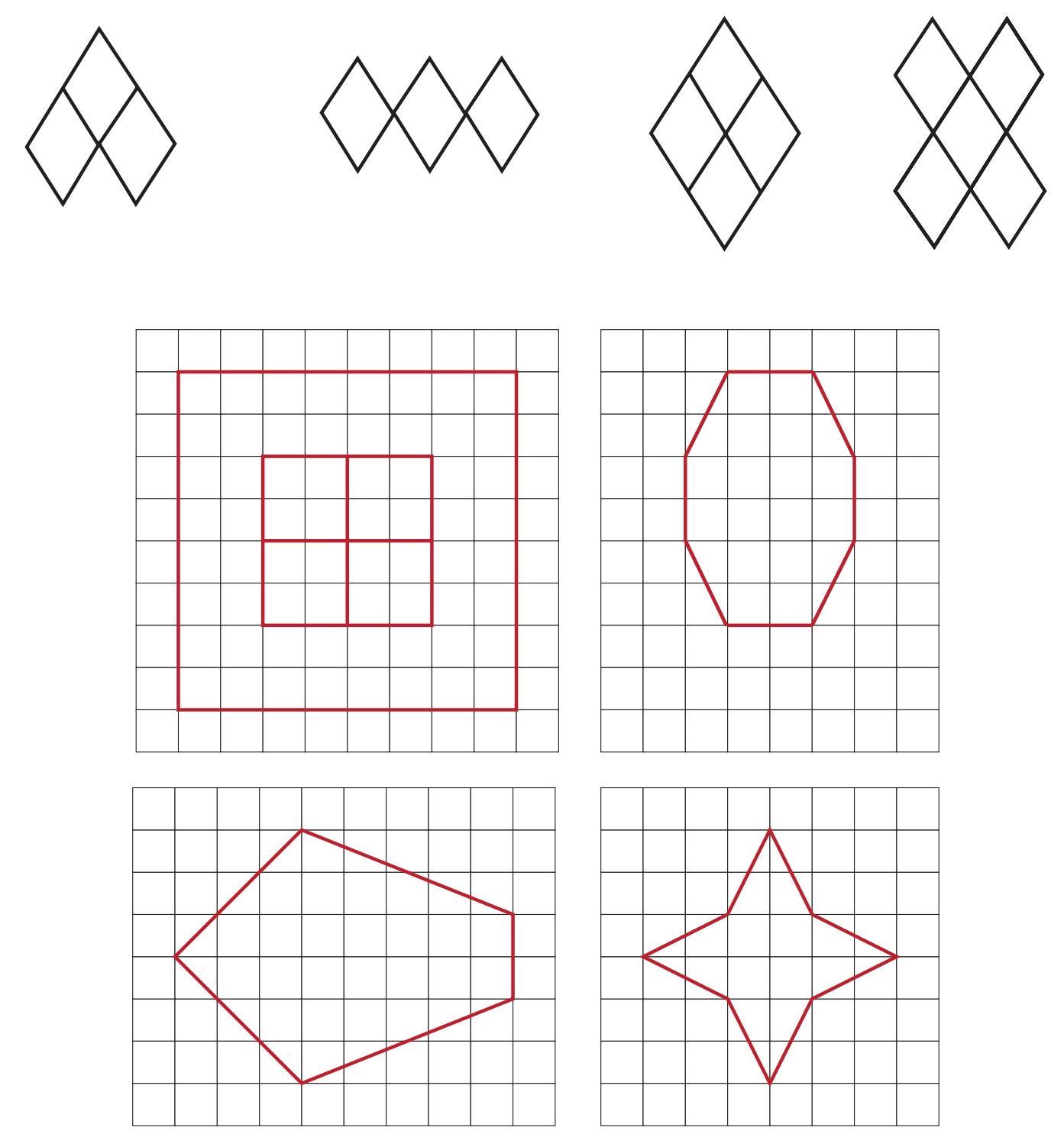
Answer:
Here are the lines of symmetry for each traced figure:
a. The arrow shape has one line of symmetry. This is a vertical line passing through the centre of the shape.
b. The crescent moon shape has one line of symmetry. This is a vertical line passing through the approximate centre of the shape.
c. The rectangle with a semi-circle cutout has one line of symmetry. This is a vertical line passing through the centre of the rectangle and the centre of the semi-circle.
d. The heart shape has one line of symmetry. This is a vertical line passing through the centre of the heart.
e. The 'E' shape has one line of symmetry. This is a horizontal line passing through the centre of the shape.
f. The cross shape has two lines of symmetry. One is a vertical line and the other is a horizontal line, both passing through the centre of the shape.
g. The circular shape with a wave pattern has one line of symmetry. This is a vertical line passing through the centre of the shape, assuming the wave pattern is symmetric vertically.
h. The 8-pointed star (assuming it is a regular star) has eight lines of symmetry. Four lines pass through opposite vertices and four lines pass through the midpoints of opposite sides.
i. The 4-lobed shape has four lines of symmetry. Two lines pass through opposite corners formed by the lobes, and two lines pass through the midpoints of the arcs between the lobes, all passing through the centre.
j. The semi-circle has one line of symmetry. This is the line that is perpendicular to the diameter and passes through the midpoint of the diameter (i.e., the radius that bisects the arc).
k. The regular pentagon has five lines of symmetry. Each line passes through a vertex and the midpoint of the opposite side.
l. The isosceles triangle has one line of symmetry. This line passes through the vertex where the two equal sides meet and the midpoint of the base.
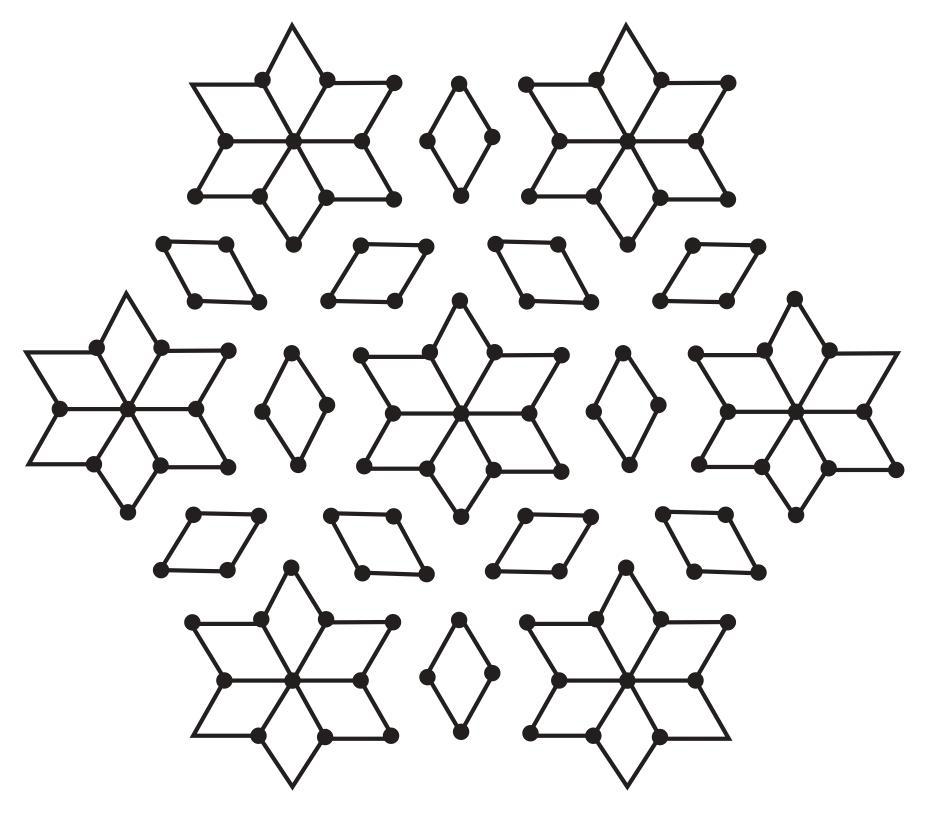
Answer:
To find the lines of symmetry for the kolam, we examine the design to see how many lines divide it into two identical mirror images.
The kolam design exhibits symmetry around its central point. By visual inspection, we can identify lines of symmetry passing through the centre.
There is a vertical line of symmetry and a horizontal line of symmetry. There are also diagonal lines of symmetry.
Due to the repeating pattern, which appears to have an 8-fold rotational symmetry, there are lines of symmetry that pass through the centre and divide the pattern into 8 identical sectors.
These lines include the vertical and horizontal lines, the two main diagonal lines (at $45^\circ$), and four additional lines that bisect the angles between these main lines.
In total, there are 8 such lines.
Therefore, the kolam has 8 lines of symmetry.
Question 9. Draw the following.
a. A triangle with exactly one line of symmetry
b. A triangle with exactly three lines of symmetry
c. A triangle with no line of symmetry
Is it possible to draw a triangle with exactly two lines of symmetry?
Answer:
Here are the descriptions and types of triangles with the specified number of lines of symmetry:
a. A triangle with exactly one line of symmetry:
This type of triangle is an isosceles triangle that is not equilateral. An isosceles triangle has two sides of equal length and the angles opposite these sides are equal. The single line of symmetry passes through the vertex where the two equal sides meet and goes to the midpoint of the opposite side (the base).
Diagram Description: Draw a triangle where two sides are equal, and the third side is different. The line of symmetry is the altitude from the vertex between the equal sides to the base.
b. A triangle with exactly three lines of symmetry:
This type of triangle is an equilateral triangle. An equilateral triangle has all three sides of equal length and all three angles equal to $60^\circ$. There are three lines of symmetry, each passing through a vertex and the midpoint of the opposite side.
Diagram Description: Draw a triangle with all sides equal. The lines of symmetry are the three medians/altitudes/angle bisectors of the triangle.
c. A triangle with no line of symmetry:
This type of triangle is a scalene triangle. A scalene triangle has all three sides of different lengths and all three angles of different measures. It does not have any line that divides it into two mirror-image halves.
Diagram Description: Draw a triangle where all three sides have different lengths.
Is it possible to draw a triangle with exactly two lines of symmetry?
No, it is not possible to draw a triangle with exactly two lines of symmetry.
A line of symmetry in a triangle is either the perpendicular bisector of a side or it passes through a vertex and the midpoint of the opposite side (which is the same line if it's an isosceles or equilateral triangle). For a triangle to have $n$ lines of symmetry, its sides and angles must be arranged in a way that supports $n$ such lines.
If a triangle had two lines of symmetry, these lines would have to meet at some point. If the lines are perpendicular, they would form a right angle at the intersection. Symmetry implies that the properties of the triangle would be reflected across these lines.
Consider the vertices. If a vertex lies on a line of symmetry, its reflection across that line is itself. If a vertex does not lie on a line of symmetry, its reflection is another vertex. Two lines of symmetry would imply that reflecting any vertex across one line, and then reflecting the result across the other line, would map to the original triangle.
For a triangle, having two lines of symmetry would force the triangle to have properties consistent with more symmetry. Specifically, if a triangle has two lines of symmetry, it must have all three sides equal (i.e., it must be equilateral), which implies it has three lines of symmetry. An isosceles triangle has one line of symmetry. A scalene triangle has zero lines of symmetry.
There is no case where a triangle has exactly two lines of symmetry.
Question 10. Draw the following. In each case, the figure should contain at least one curved boundary.
a. A figure with exactly one line of symmetry
b. A figure with exactly two lines of symmetry
c. A figure with exactly four lines of symmetry
Answer:
Here are examples of figures with at least one curved boundary and the specified number of lines of symmetry:
a. A figure with exactly one line of symmetry:
A simple example is a semi-circle. It has one curved boundary (the arc) and one straight boundary (the diameter).
Description of lines of symmetry: The single line of symmetry is the line perpendicular to the diameter that passes through the midpoint of the diameter (which is also the centre of the circle from which the semi-circle is formed). This line is the radius that bisects the arc.
b. A figure with exactly two lines of symmetry:
An example is an oval (ellipse) that is not a circle.
Description of lines of symmetry: An ellipse has two lines of symmetry: its major axis and its minor axis. These lines are perpendicular to each other and pass through the centre of the ellipse.
Another example could be a rectangle with a semi-circle attached to each of its two opposite sides, or a shape like a running track oval.
c. A figure with exactly four lines of symmetry:
An example is a square with four identical semi-circles attached outwards on each side, centered on the midpoint of each side. This creates a shape with a curved boundary made of four semi-circles.
Description of lines of symmetry: This shape will inherit the symmetries of the underlying square. It has four lines of symmetry: two lines passing through the midpoints of opposite pairs of sides (horizontal and vertical) and two lines passing through opposite vertices (the diagonals of the original square). All four lines pass through the centre of the square.
Another example is a circle with a concentric square inscribed or circumscribed, but the question requires the figure itself to have at least one curved boundary, so a square outline is not sufficient unless the boundary is the curved part. A square with rounded corners (formed by quarter circles) or a shape like a four-leaf clover (quatrefoil) also has four lines of symmetry and a curved boundary.
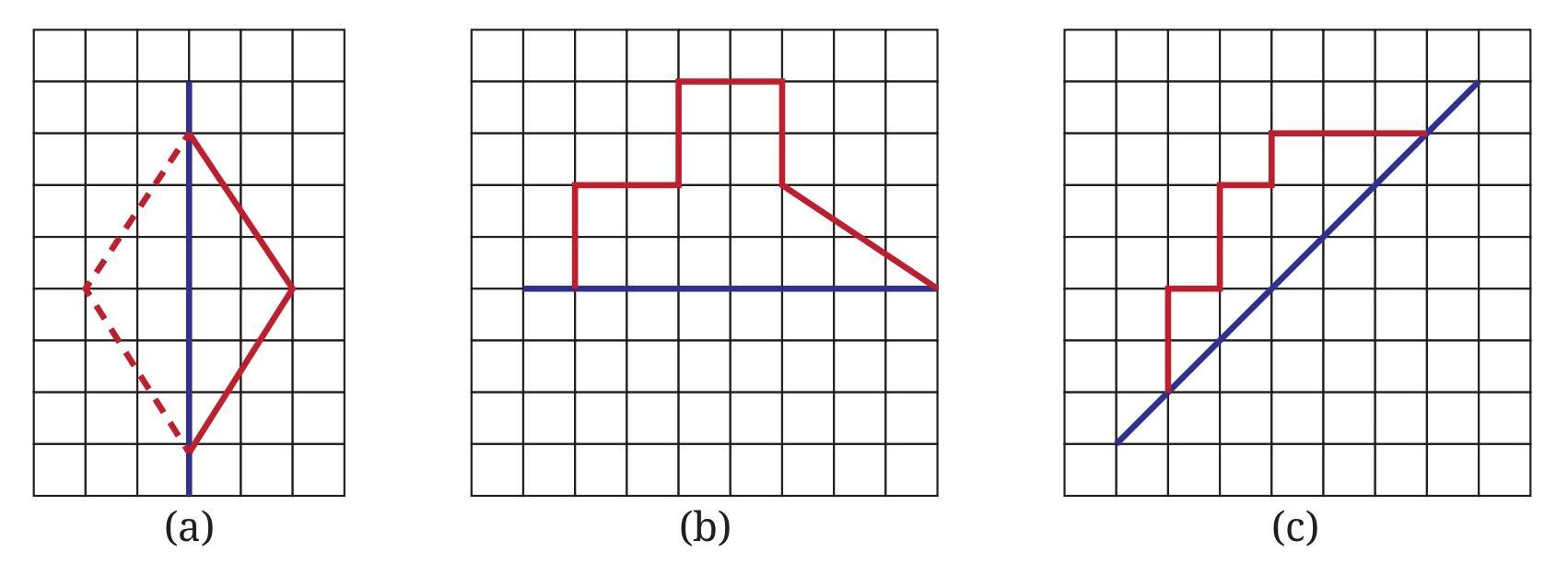
Answer:
To complete each figure such that the blue line is a line of symmetry, we need to draw the mirror image of the given part across the blue line.
a. Figure (a):
This problem has been done for you in the image. The given shape is reflected across the vertical blue line. Each point on the left side of the blue line is mirrored to a corresponding point on the right side, at the same perpendicular distance from the line.
b. Figure (b):
The blue line is horizontal. The given part is above the blue line. To complete the figure, reflect each point and segment of the given shape downwards across the blue line. If a point is $n$ units above the blue line, its reflected point will be $n$ units below the blue line along the same vertical line. This will create a symmetrical shape below the horizontal blue line.
c. Figure (c):
The blue line is vertical. The given part is to the left of the blue line. To complete the figure, reflect each point and segment of the given shape horizontally across the blue line to the right. If a point is $n$ units to the left of the blue line, its reflected point will be $n$ units to the right of the blue line along the same horizontal line. This will create a symmetrical shape to the right of the vertical blue line.
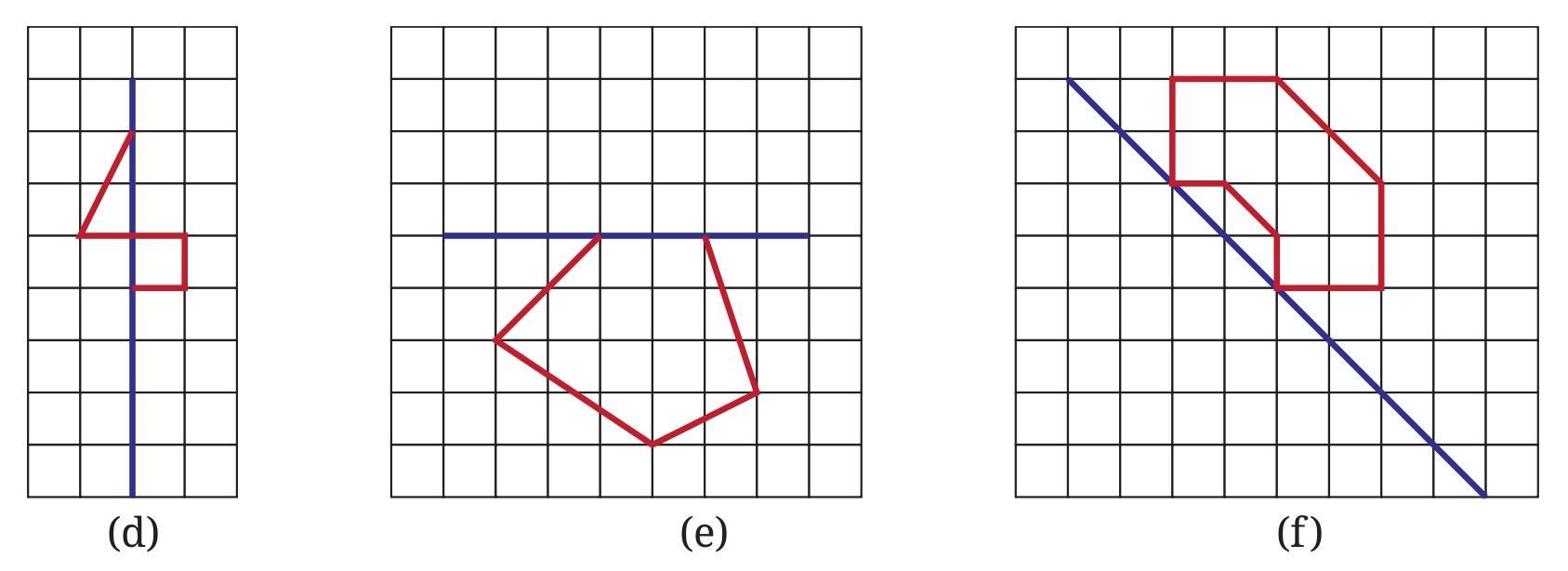
d. Figure (d):
The blue line is a diagonal line. The given part is above and to the left of the diagonal blue line. To complete the figure, reflect each point and segment of the given shape across the diagonal blue line. For reflection across a diagonal line, the perpendicular distance from a point to the line of symmetry is the same as the perpendicular distance from the reflected point to the line. This requires counting squares diagonally relative to the line.
e. Figure (e):
The blue line is a diagonal line. The given part is below and to the left of the diagonal blue line. Similar to part (d), reflect each point and segment of the given shape across the diagonal blue line to complete the symmetrical figure. Use the property that the line of symmetry is the perpendicular bisector of the segment connecting a point and its image.
f. Figure (f):
The blue line is vertical. The given part is to the left of the blue line. Reflect each point and segment of the given shape horizontally across the blue line to the right, similar to part (c). The completed figure will be symmetrical about the vertical blue line.
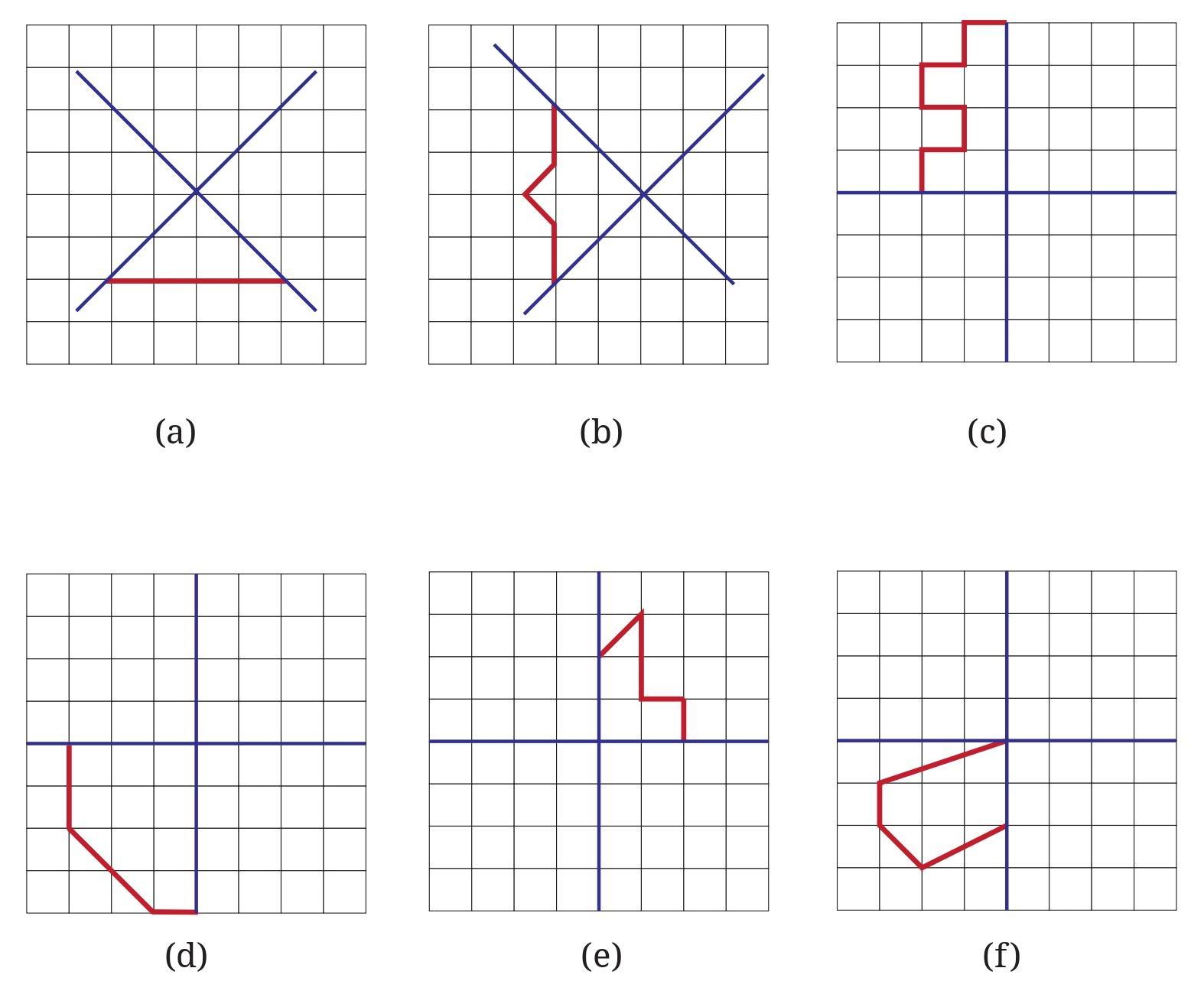
Answer:
To complete each figure such that the two blue lines are lines of symmetry, we need to ensure that the final shape is symmetrical with respect to both the horizontal and the vertical blue lines.
The two blue lines intersect, dividing the squared paper into four sections or quadrants. The given part of the figure is located in one of these sections.
To achieve symmetry about both lines, we need to draw the reflection of the given part in each of the other three sections.
Method:
1. Identify the given part of the figure.
2. Reflect the given part across the horizontal blue line. Draw this reflected shape in the section adjacent across the horizontal line.
3. Reflect the original given part across the vertical blue line. Draw this reflected shape in the section adjacent across the vertical line.
4. Reflect either of the shapes drawn in steps 2 or 3 across the other blue line. For example, reflect the shape from step 2 (reflected across horizontal) across the vertical line. This will fill the remaining section.
Alternatively, you can think of reflecting the original shape across both lines sequentially. Reflecting across the horizontal line followed by reflecting across the vertical line (or vice versa) is equivalent to rotating the original shape by $180^\circ$ around the point where the two blue lines intersect.
For figures (a), (b), and (c):
In each case, the given part is in one quadrant. The two blue lines are the horizontal and vertical axes of symmetry. Apply the method described above:
- Draw the reflection of the given shape across the horizontal blue line.
- Draw the reflection of the given shape across the vertical blue line.
- Draw the reflection of the given shape (or one of the previously reflected shapes) into the fourth quadrant to complete the symmetry.
The resulting figure will be symmetrical about both the horizontal and vertical blue lines.
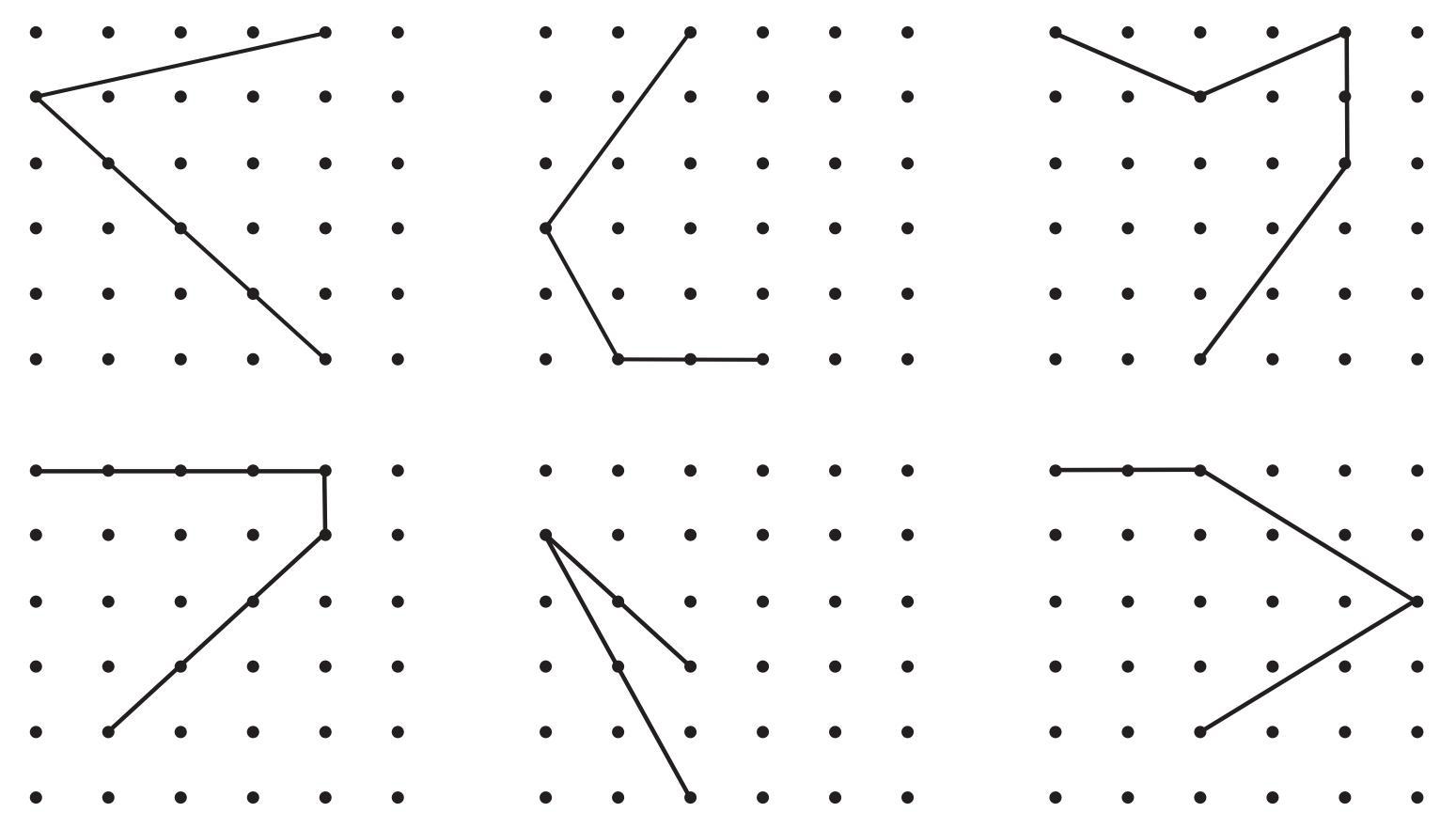
Answer:
To complete each figure on the dot grid using exactly two more lines such that the resulting shape has a line of symmetry, we need to add lines that, along with the given lines, form a symmetrical shape. Here's one way to do it for each figure:
a.
The given shape is like an inverted 'V'. It consists of two segments meeting at an upper vertex, with the other two endpoints horizontally aligned.
Added lines:
1. Add a horizontal line connecting the two lower endpoint dots of the original shape.
2. Add a vertical line from the top vertex dot downwards to the midpoint of the horizontal line just drawn. (Assuming the vertex is vertically above the midpoint of the base formed by the endpoints, which is typical for such grid patterns).
The resulting shape is an isosceles triangle, which has a vertical line of symmetry passing through the top vertex.
b.
The given shape is like an 'L'. It consists of a vertical segment and a horizontal segment meeting at a corner.
Added lines:
1. Connect the bottom-leftmost dot (the start of the vertical segment) to the rightmost dot directly below the end of the horizontal segment. This adds a horizontal line.
2. Connect the dot just added (the bottom-right corner) upwards to the end dot of the horizontal segment. This adds a vertical line.
The resulting shape is a rectangle, which has both horizontal and vertical lines of symmetry.
c.
The given shape is a step-like zig-zag line.
Added lines:
1. Draw a horizontal line from the top-leftmost dot straight across to the right, connecting to a dot three units to the right.
2. Draw a vertical line from the dot just added downwards to the bottom-rightmost dot of the original shape.
The resulting shape is a polygon that is symmetrical about a horizontal line passing through its vertical centre.
d.
The given shape consists of two diagonal segments meeting at a point, forming a shallow 'V' pointing downwards.
Added lines:
1. Connect the two upper endpoint dots with a horizontal line.
2. Draw a vertical line from the lower vertex dot upwards to the midpoint of the horizontal line just drawn.
The resulting shape is an isosceles triangle, which has a vertical line of symmetry passing through the lower vertex.
e.
This figure is identical to figure (b).
Added lines:
1. Connect the bottommost dot (the start of the vertical segment) to the rightmost dot directly below the end of the horizontal segment. This adds a horizontal line.
2. Connect the dot just added (the bottom-right corner) upwards to the end dot of the horizontal segment. This adds a vertical line.
The resulting shape is a rectangle, which has both horizontal and vertical lines of symmetry.
f.
The given shape consists of two diagonal segments meeting at a point, forming a shape like '<'.
Added lines:
1. Connect the two leftmost endpoint dots with a vertical line.
2. Draw a horizontal line from the rightmost vertex dot leftwards to the midpoint of the vertical line just drawn.
The resulting shape is an isosceles triangle (rotated), which has a horizontal line of symmetry passing through the rightmost vertex.
Figure it Out (Page 235 - 236)
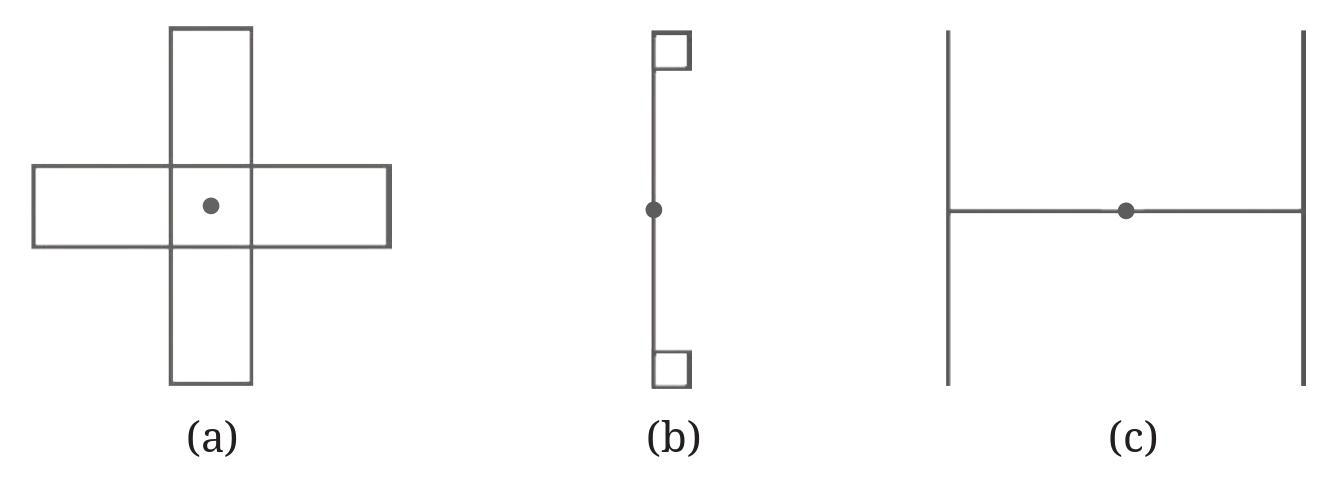
Answer:
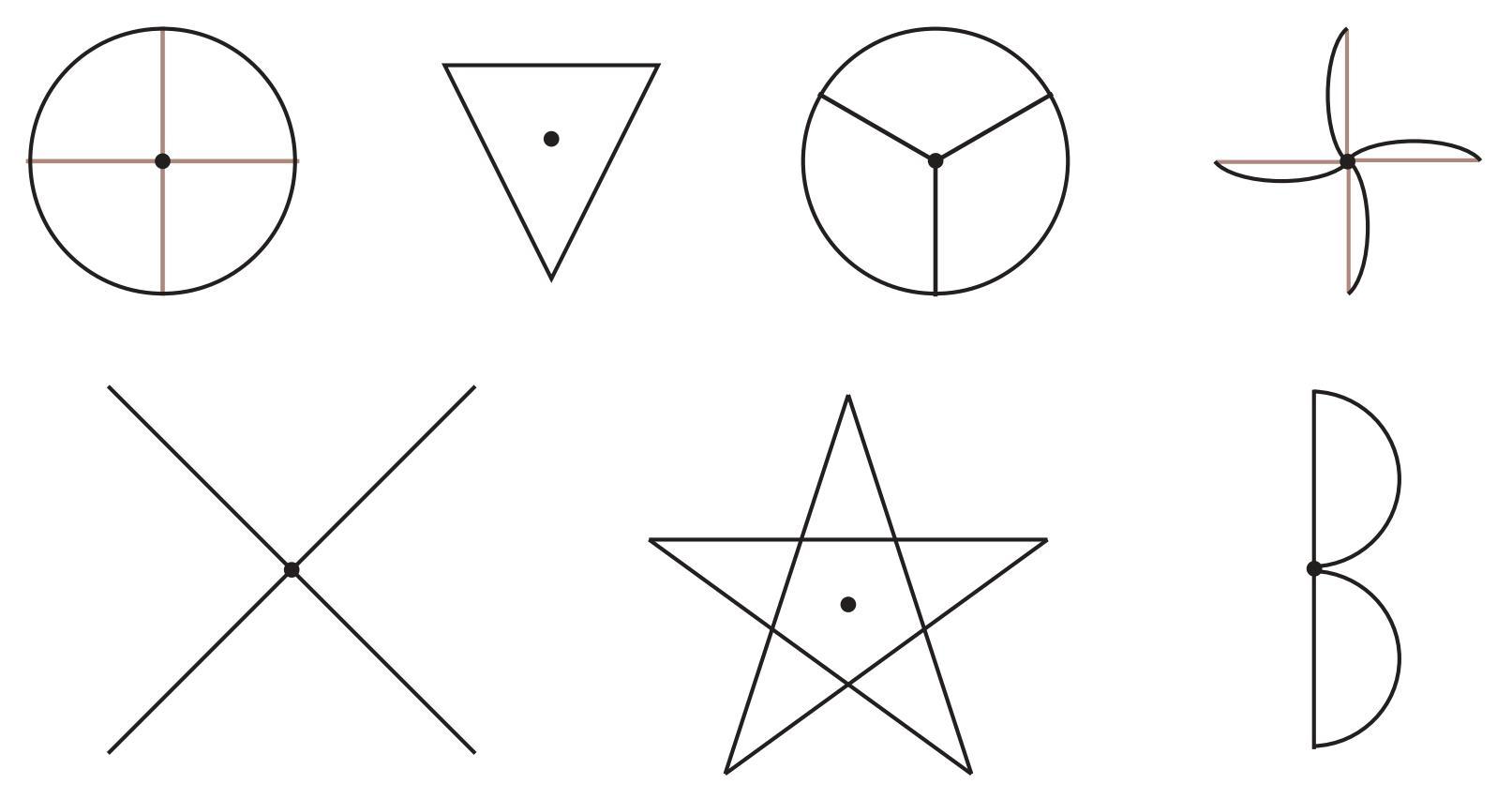
To find the angles of rotational symmetry for each figure about the marked point, we determine the angles (between $0^\circ$ and $360^\circ$) through which the figure can be rotated so that it coincides with its original position.
a.
The figure is a capital 'H'. Rotating it by $180^\circ$ about its center makes it look identical to the original position.
The angles of rotational symmetry are $180^\circ$ and $360^\circ$.
b.
The figure is a Yin Yang symbol. Rotating it by $180^\circ$ about its center makes it look identical to the original position.
The angles of rotational symmetry are $180^\circ$ and $360^\circ$.
c.
The figure is a three-bladed shape with rotational symmetry. Since there are 3 identical parts, the smallest angle of rotation is $360^\circ / 3 = 120^\circ$.
The angles of rotational symmetry are $120^\circ$, $240^\circ$, and $360^\circ$.
d.
The figure is a shape with four-fold rotational symmetry. Since there are 4 identical parts, the smallest angle of rotation is $360^\circ / 4 = 90^\circ$.
The angles of rotational symmetry are $90^\circ$, $180^\circ$, $270^\circ$, and $360^\circ$.
e.
The figure is a swastika symbol, which has four-fold rotational symmetry. Since there are 4 repeating elements, the smallest angle of rotation is $360^\circ / 4 = 90^\circ$.
The angles of rotational symmetry are $90^\circ$, $180^\circ$, $270^\circ$, and $360^\circ$.
f.
The figure is a shape with six-fold rotational symmetry. Since there are 6 identical parts, the smallest angle of rotation is $360^\circ / 6 = 60^\circ$.
The angles of rotational symmetry are $60^\circ$, $120^\circ$, $180^\circ$, $240^\circ$, $300^\circ$, and $360^\circ$.
g.
The figure is a regular pentagon. A regular pentagon has five-fold rotational symmetry. Since there are 5 equal sides/vertices, the smallest angle of rotation is $360^\circ / 5 = 72^\circ$.
The angles of rotational symmetry are $72^\circ$, $144^\circ$, $216^\circ$, $288^\circ$, and $360^\circ$.
h.
The figure is a circle. A circle has rotational symmetry about its center for any angle of rotation. Thus, it has infinite rotational symmetry.
The angles of rotational symmetry include any angle $\theta$ where $0^\circ < \theta \leq 360^\circ$.
Answer:
We need to identify which of the given figures have more than one angle of rotational symmetry about the marked point.
The angles of rotational symmetry are the angles (between $0^\circ$ and $360^\circ$, inclusive of $360^\circ$) through which the figure can be rotated about the marked point to coincide with its original position.
Let's list the angles of symmetry for each figure (from Question 1):
a. Figure (a) (Capital 'H'): Angles of symmetry are $180^\circ$, $360^\circ$. This is 2 angles.
b. Figure (b) (Yin Yang): Angles of symmetry are $180^\circ$, $360^\circ$. This is 2 angles.
c. Figure (c) (Three-bladed shape): Angles of symmetry are $120^\circ$, $240^\circ$, $360^\circ$. This is 3 angles.
d. Figure (d) (Four-fold shape): Angles of symmetry are $90^\circ$, $180^\circ$, $270^\circ$, $360^\circ$. This is 4 angles.
e. Figure (e) (Swastika): Angles of symmetry are $90^\circ$, $180^\circ$, $270^\circ$, $360^\circ$. This is 4 angles.
f. Figure (f) (Six-fold shape): Angles of symmetry are $60^\circ$, $120^\circ$, $180^\circ$, $240^\circ$, $300^\circ$, $360^\circ$. This is 6 angles.
g. Figure (g) (Regular pentagon): Angles of symmetry are $72^\circ$, $144^\circ$, $216^\circ$, $288^\circ$, $360^\circ$. This is 5 angles.
h. Figure (h) (Circle): Angles of symmetry are all angles $\theta$ such that $0^\circ < \theta \leq 360^\circ$. This is an infinite number of angles.
Comparing the number of angles of symmetry for each figure, we see that:
- Figure (a) has 2 angles of symmetry, which is more than one.
- Figure (b) has 2 angles of symmetry, which is more than one.
- Figure (c) has 3 angles of symmetry, which is more than one.
- Figure (d) has 4 angles of symmetry, which is more than one.
- Figure (e) has 4 angles of symmetry, which is more than one.
- Figure (f) has 6 angles of symmetry, which is more than one.
- Figure (g) has 5 angles of symmetry, which is more than one.
- Figure (h) has infinitely many angles of symmetry, which is more than one.
Therefore, all the figures have more than one angle of symmetry.
The figures that have more than one angle of symmetry are: (a), (b), (c), (d), (e), (f), (g), and (h).
Question 3. Give the order of rotational symmetry for each figure:
Let us list down the angles of symmetry for all the cases above .
- Angles of symmetry when there are exactly 2 of them: 180°, 360°.
- Angles of symmetry when there are exactly 3 of them: 120°, 240°, 360°.
- Angles of symmetry when there are exactly 4 of them: 90°, 180°, 270°, 360°.
Answer:
The order of rotational symmetry is the number of times a figure looks exactly the same during a full rotation of $360^\circ$ about its center of rotation.
a.
The figure is a capital 'H'. It matches its original position after a $180^\circ$ rotation and a $360^\circ$ rotation. The smallest angle of rotation is $180^\circ$. The order is $360^\circ / 180^\circ = 2$.
Order of rotational symmetry is 2.
b.
The figure is a Yin Yang symbol. It matches its original position after a $180^\circ$ rotation and a $360^\circ$ rotation. The smallest angle of rotation is $180^\circ$. The order is $360^\circ / 180^\circ = 2$.
Order of rotational symmetry is 2.
c.
The figure is a three-bladed shape. It matches its original position after rotations of $120^\circ$, $240^\circ$, and $360^\circ$. The smallest angle of rotation is $120^\circ$. The order is $360^\circ / 120^\circ = 3$.
Order of rotational symmetry is 3.
d.
The figure has four-fold rotational symmetry. It matches its original position after rotations of $90^\circ$, $180^\circ$, $270^\circ$, and $360^\circ$. The smallest angle of rotation is $90^\circ$. The order is $360^\circ / 90^\circ = 4$.
Order of rotational symmetry is 4.
e.
The figure is a swastika symbol. It has four-fold rotational symmetry. It matches its original position after rotations of $90^\circ$, $180^\circ$, $270^\circ$, and $360^\circ$. The smallest angle of rotation is $90^\circ$. The order is $360^\circ / 90^\circ = 4$.
Order of rotational symmetry is 4.
f.
The figure has six-fold rotational symmetry. It matches its original position after rotations of $60^\circ$, $120^\circ$, $180^\circ$, $240^\circ$, $300^\circ$, and $360^\circ$. The smallest angle of rotation is $60^\circ$. The order is $360^\circ / 60^\circ = 6$.
Order of rotational symmetry is 6.
g.
The figure is a regular pentagon. It has five-fold rotational symmetry. It matches its original position after rotations of $72^\circ$, $144^\circ$, $216^\circ$, $288^\circ$, and $360^\circ$. The smallest angle of rotation is $72^\circ$. The order is $360^\circ / 72^\circ = 5$.
Order of rotational symmetry is 5.
h.
The figure is a circle. It matches its original position after rotation through any angle about its center. It has infinite rotational symmetry.
Order of rotational symmetry is infinite.
Figure it Out (Page 238)
Question 1. Color the sectors of the circle below so that the figure has
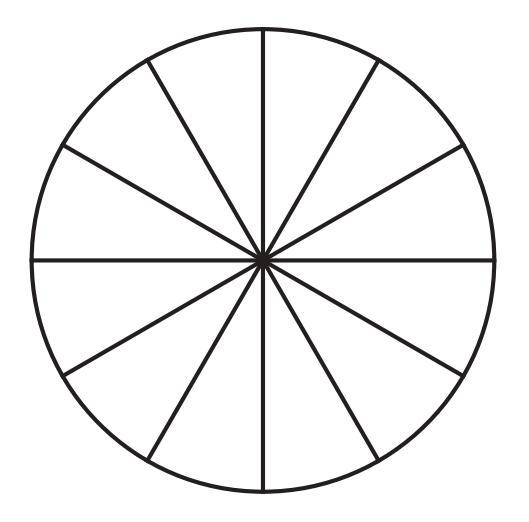
i) 3 angles of symmetry,
ii) 4 angles of symmetry,
iii) what are the possible numbers of angles of symmetry you can obtain by coloring the sectors in different ways?
Answer:
The circle is divided into 12 equal sectors. Each sector has an angle of $360^\circ / 12 = 30^\circ$. Rotational symmetry occurs when the colored figure coincides with its original position after a rotation about the center.
The angles of rotational symmetry must be multiples of the smallest angle needed to rotate one sector onto an adjacent sector, which is $30^\circ$. However, the angles of symmetry are determined by the repeating pattern of colors. If the pattern repeats every $k$ sectors, the smallest angle of rotational symmetry will be $k \times 30^\circ$. The order of rotational symmetry, $n$, is $360^\circ / (k \times 30^\circ) = 12/k$. For $n$ to be an integer, $k$ must be a divisor of 12 (where $k$ is the number of sectors in the repeating unit pattern). Conversely, the smallest angle of rotational symmetry is $360^\circ/n$, where $n$ is the order of symmetry. For this angle to be a multiple of $30^\circ$, $n$ must be a divisor of $360/30 = 12$.
The possible orders of rotational symmetry are the divisors of 12: 1, 2, 3, 4, 6, 12. The number of angles of symmetry (including $360^\circ$) is equal to the order of rotational symmetry.
i) Color the sectors so that the figure has 3 angles of symmetry:
This requires an order of rotational symmetry of 3. The smallest angle of rotation is $360^\circ / 3 = 120^\circ$. This means the coloring pattern must repeat every $120^\circ$. Since each sector is $30^\circ$, $120^\circ$ corresponds to $120^\circ / 30^\circ = 4$ sectors.
Coloring Method: Divide the 12 sectors into 3 groups of 4 sectors each (sectors 1-4, 5-8, 9-12). Color the sectors in each group with the same sequence of colors. For example, color sectors 1, 5, 9 Red; sectors 2, 6, 10 Blue; sectors 3, 7, 11 Green; and sectors 4, 8, 12 Yellow.
Angles of symmetry: $120^\circ$, $240^\circ$, $360^\circ$. There are 3 angles.
ii) Color the sectors so that the figure has 4 angles of symmetry:
This requires an order of rotational symmetry of 4. The smallest angle of rotation is $360^\circ / 4 = 90^\circ$. This means the coloring pattern must repeat every $90^\circ$. Since each sector is $30^\circ$, $90^\circ$ corresponds to $90^\circ / 30^\circ = 3$ sectors.
Coloring Method: Divide the 12 sectors into 4 groups of 3 sectors each (sectors 1-3, 4-6, 7-9, 10-12). Color the sectors in each group with the same sequence of colors. For example, color sectors 1, 4, 7, 10 Red; sectors 2, 5, 8, 11 Blue; and sectors 3, 6, 9, 12 Green.
Angles of symmetry: $90^\circ$, $180^\circ$, $270^\circ$, $360^\circ$. There are 4 angles.
iii) What are the possible numbers of angles of symmetry you can obtain by coloring the sectors in different ways?
The number of angles of rotational symmetry (including $360^\circ$) is equal to the order of rotational symmetry. For a figure composed of 12 equally spaced sectors colored such that the pattern repeats, the order of rotational symmetry must be a divisor of the total number of sectors, 12.
The divisors of 12 are 1, 2, 3, 4, 6, and 12.
Therefore, the possible numbers of angles of symmetry are the possible orders of rotational symmetry, which are 1, 2, 3, 4, 6, and 12.
Examples of coloring for each possible number of angles of symmetry:
- Order 1 (1 angle: $360^\circ$): Color one sector differently from all the others (e.g., one Red, eleven Blue).
- Order 2 (2 angles: $180^\circ$, $360^\circ$): Color the first 6 sectors in some pattern and the next 6 sectors exactly the same (e.g., sectors 1-6 Red, sectors 7-12 Red). Or color sectors 1, 3, 5, 7, 9, 11 Red and 2, 4, 6, 8, 10, 12 Blue.
- Order 3 (3 angles: $120^\circ$, $240^\circ$, $360^\circ$): Color the first 4 sectors in some pattern and repeat it for the next two groups of 4 (as described in part i).
- Order 4 (4 angles: $90^\circ$, $180^\circ$, $270^\circ$, $360^\circ$): Color the first 3 sectors in some pattern and repeat it for the next three groups of 3 (as described in part ii).
- Order 6 (6 angles: $60^\circ$, $120^\circ$, $180^\circ$, $240^\circ$, $300^\circ$, $360^\circ$): Color the first 2 sectors in some pattern and repeat it for the next five groups of 2 (e.g., sectors 1, 3, 5, 7, 9, 11 Red and sectors 2, 4, 6, 8, 10, 12 Blue).
- Order 12 (12 angles: $30^\circ$, $60^\circ$, ..., $360^\circ$): Color all 12 sectors with the same color.
Question 2. Draw two figures other than a circle and a square that have both reflection symmetry and rotational symmetry.
Answer:
Here are two figures, other than a circle and a square, that have both reflection symmetry and rotational symmetry:
Figure 1: A Rectangle (that is not a square)
A rectangle has four sides and four right angles. If the adjacent sides are of different lengths, it is not a square.
Reflection Symmetry: A rectangle has exactly two lines of reflection symmetry. These lines pass through the midpoints of opposite sides.
Rotational Symmetry: A rectangle has rotational symmetry of order 2. It can be rotated by $180^\circ$ about the intersection point of its diagonals (its center) and look exactly the same.
Figure 2: A Regular Hexagon
A regular hexagon is a six-sided polygon where all sides are equal in length and all interior angles are equal ($120^\circ$).
Reflection Symmetry: A regular hexagon has exactly six lines of reflection symmetry. Three lines pass through opposite pairs of vertices, and three lines pass through the midpoints of opposite pairs of sides.
Rotational Symmetry: A regular hexagon has rotational symmetry of order 6. It can be rotated by $60^\circ$ (which is $360^\circ / 6$) and its multiples ($120^\circ, 180^\circ, 240^\circ, 300^\circ, 360^\circ$) about its center and look exactly the same.
Other examples include a rhombus (not a square), a regular pentagon, a regular octagon, or an ellipse (not a circle).
Question 3. Draw, wherever possible, a rough sketch of
a. A triangle with at least two lines of symmetry and at least two angles of symmetry.
b. A triangle with only one line of symmetry but not having rotational symmetry.
c. A quadrilateral with rotational symmetry but no reflection symmetry.
d. A quadrilateral with reflection symmetry but not having rotational symmetry.
Answer:
Here are the rough sketches and descriptions for the requested figures:
a. A triangle with at least two lines of symmetry and at least two angles of symmetry.
A triangle with at least two lines of symmetry must have exactly three lines of symmetry (passing through each vertex and the midpoint of the opposite side). This type of triangle is an equilateral triangle.
An equilateral triangle has rotational symmetry of order 3 about its centroid. This means it has 3 angles of symmetry: $120^\circ$, $240^\circ$, and $360^\circ$. Having 3 angles of symmetry satisfies the condition of having at least two angles of symmetry.
Therefore, the required triangle is an equilateral triangle.
Rough Sketch: Draw a triangle with all three sides appearing equal in length and all three angles appearing equal ($60^\circ$).
b. A triangle with only one line of symmetry but not having rotational symmetry.
A triangle with exactly one line of symmetry is an isosceles triangle that is not equilateral. The line of symmetry passes through the vertex formed by the two equal sides and the midpoint of the base.
An isosceles triangle that is not equilateral has rotational symmetry of order 1 only (i.e., only the $360^\circ$ rotation maps it onto itself). It does not have rotational symmetry for any angle other than $360^\circ$. Thus, it does not have rotational symmetry in the sense of having more than one angle of symmetry.
Therefore, the required triangle is a non-equilateral isosceles triangle.
Rough Sketch: Draw a triangle with two sides of equal length and the third side of a different length. The angles opposite the equal sides should be equal, and the third angle should be different.
c. A quadrilateral with rotational symmetry but no reflection symmetry.
A quadrilateral that has rotational symmetry but no reflection symmetry is a parallelogram that is neither a rhombus nor a rectangle.
A parallelogram has rotational symmetry of order 2 about the intersection of its diagonals. It coincides with itself after a $180^\circ$ rotation and a $360^\circ$ rotation. Thus, it has rotational symmetry (2 angles of symmetry).
However, a parallelogram has reflection symmetry only if it is a rhombus (symmetry along diagonals) or a rectangle (symmetry through midpoints of sides). A general parallelogram with unequal adjacent sides and non-right angles does not have reflection symmetry.
Rough Sketch: Draw a four-sided figure with opposite sides parallel and equal in length, but with no right angles and unequal adjacent sides. For example, draw a shape like a 'squashed' rectangle.
d. A quadrilateral with reflection symmetry but not having rotational symmetry.
A quadrilateral with reflection symmetry but not having rotational symmetry (other than order 1, i.e., only $360^\circ$) can be a kite that is not a rhombus or an isosceles trapezoid.
Let's consider an isosceles trapezoid:
Reflection Symmetry: An isosceles trapezoid has exactly one line of reflection symmetry. This line passes through the midpoints of the two parallel sides.
Rotational Symmetry: An isosceles trapezoid has rotational symmetry of order 1 only. No rotation other than $360^\circ$ maps it onto itself (unless it is a rectangle or square, which have rotational symmetry).
Therefore, an isosceles trapezoid fits the description.
Rough Sketch: Draw a four-sided figure with exactly one pair of parallel sides (the bases) and the two non-parallel sides equal in length. The base angles on each parallel side are equal.
Let's consider a kite that is not a rhombus:
Reflection Symmetry: A kite has reflection symmetry along one of its diagonals (the diagonal between the vertices where equal sides meet). If it is not a rhombus, it has exactly one such line of symmetry.
Rotational Symmetry: A kite has rotational symmetry of order 1 only (unless it is a rhombus or square, which have rotational symmetry). No rotation other than $360^\circ$ maps it onto itself.
Therefore, a kite that is not a rhombus also fits the description.
Rough Sketch: Draw a quadrilateral with two pairs of equal-length sides that are adjacent to each other. The vertices where the unequal sides meet are connected by a line of symmetry. The diagonals are perpendicular, but only one diagonal is a line of symmetry.
Question 4. In a figure, 60° is the smallest angle of symmetry. What are the other angles of symmetry of this figure?
Answer:
If $60^\circ$ is the smallest angle of rotational symmetry for a figure, it means that the figure coincides with itself when rotated by $60^\circ$ about its center of rotation.
Any other angle of rotational symmetry for this figure must be a multiple of the smallest angle of symmetry, within a full rotation of $360^\circ$.
The angles of rotation that produce symmetry are $k \times 60^\circ$, where $k$ is a positive integer such that $k \times 60^\circ \leq 360^\circ$.
Let's list these multiples:
$1 \times 60^\circ = 60^\circ$
$2 \times 60^\circ = 120^\circ$
$3 \times 60^\circ = 180^\circ$
$4 \times 60^\circ = 240^\circ$
$5 \times 60^\circ = 300^\circ$
$6 \times 60^\circ = 360^\circ$
The angles of rotational symmetry are $60^\circ, 120^\circ, 180^\circ, 240^\circ, 300^\circ$, and $360^\circ$. The order of rotational symmetry is 6.
The question asks for the other angles of symmetry, excluding the smallest one ($60^\circ$).
Therefore, the other angles of symmetry are:
$120^\circ$, $180^\circ$, $240^\circ$, $300^\circ$, and $360^\circ$.
Question 5. In a figure, 60° is an angle of symmetry. The figure has two angles of symmetry less than 60°. What is its smallest angle of symmetry?
Answer:
Let the smallest angle of rotational symmetry of the figure be $\alpha$.
All angles of rotational symmetry for a figure are positive integer multiples of its smallest angle of symmetry $\alpha$. These angles are $\alpha, 2\alpha, 3\alpha, \dots, n\alpha = 360^\circ$, where $n$ is the order of rotational symmetry.
We are given that $60^\circ$ is an angle of symmetry. This means $60^\circ$ must be a multiple of the smallest angle $\alpha$. So, we can write $60^\circ = k \times \alpha$ for some positive integer $k \ge 1$.
We are also given that the figure has exactly two angles of symmetry less than $60^\circ$. Since all angles of symmetry are multiples of $\alpha$, the angles less than $60^\circ$ must be the first few multiples of $\alpha$ that are less than $60^\circ$.
The angles of symmetry, in increasing order, start with $\alpha, 2\alpha, 3\alpha, \dots$. The two angles of symmetry less than $60^\circ$ must therefore be $\alpha$ and $2\alpha$.
This implies two conditions:
1. The second multiple of $\alpha$ is less than $60^\circ$: $2\alpha < 60^\circ$.
2. The third multiple of $\alpha$ is not less than $60^\circ$ (otherwise there would be three or more angles less than $60^\circ$): $3\alpha \ge 60^\circ$.
From the first inequality:
$2\alpha < 60^\circ$
$\alpha < \frac{60^\circ}{2}$
$\alpha < 30^\circ $
... (i)
From the second inequality:
$3\alpha \ge 60^\circ$
$\alpha \ge \frac{60^\circ}{3}$
$\alpha \ge 20^\circ$
... (ii)
Combining conditions (i) and (ii), the smallest angle $\alpha$ must satisfy $20^\circ \le \alpha < 30^\circ$.
We also know that $60^\circ$ is a multiple of $\alpha$, so $\alpha$ must be a divisor of $60^\circ$. We need to find a divisor of $60^\circ$ that lies in the range $[20^\circ, 30^\circ)$.
Possible divisors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
The corresponding possible values for $\alpha$ are $60^\circ/1=60^\circ$, $60^\circ/2=30^\circ$, $60^\circ/3=20^\circ$, $60^\circ/4=15^\circ$, etc.
We look for a value in the range $20^\circ \le \alpha < 30^\circ$.
- If $\alpha = 60^\circ$, it's not less than $30^\circ$.
- If $\alpha = 30^\circ$, it's not less than $30^\circ$.
- If $\alpha = 20^\circ$, it satisfies $20^\circ \le 20^\circ < 30^\circ$. Let's check if this value works.
- If $\alpha = 15^\circ$, it is less than $20^\circ$.
- Other smaller divisors will give smaller $\alpha$ values, which are also less than $20^\circ$.
The only value that satisfies both conditions ($20^\circ \le \alpha < 30^\circ$ and $\alpha$ is a divisor of $60^\circ$) is $\alpha = 20^\circ$.
Let's verify if the smallest angle of symmetry is $20^\circ$ satisfies the original conditions:
If $\alpha = 20^\circ$, the angles of symmetry are multiples of $20^\circ$: $20^\circ, 40^\circ, 60^\circ, 80^\circ, \dots, 360^\circ$.
- Is $60^\circ$ an angle of symmetry? Yes, $60^\circ = 3 \times 20^\circ$.
- Are there exactly two angles of symmetry less than $60^\circ$? Yes, $20^\circ$ and $40^\circ$ are the angles of symmetry less than $60^\circ$. There are exactly two such angles.
Both conditions are satisfied.
Thus, the smallest angle of symmetry is $20^\circ$.
Question 6. Can we have a figure with rotational symmetry whose smallest angle of symmetry is
a. 45°
b. 17°
Answer:
For a figure to have rotational symmetry with a smallest angle of symmetry $\alpha$, every rotation by an integer multiple of $\alpha$ up to $360^\circ$ must result in the figure coinciding with itself. The rotation by $360^\circ$ must always bring the figure back to its original position, so $360^\circ$ must be an angle of symmetry. This implies that $360^\circ$ must be an integer multiple of the smallest angle of symmetry $\alpha$. Mathematically, $360^\circ = n \times \alpha$, where $n$ is the order of rotational symmetry (a positive integer).
Therefore, a figure can have a smallest angle of symmetry $\alpha$ if and only if $\alpha$ is a divisor of $360^\circ$ (i.e., $360/\alpha$ is an integer).
a. Can we have a figure with rotational symmetry whose smallest angle of symmetry is 45°?
To check this, we see if $360^\circ$ is divisible by $45^\circ$.
$\frac{360^\circ}{45^\circ} = \frac{360}{45} $
We can perform the division:
$\frac{360}{45} = \frac{72 \times 5}{9 \times 5} = \frac{72}{9} = 8$
Since $360/45 = 8$, which is an integer, $45^\circ$ is a divisor of $360^\circ$.
This means it is possible to have a figure with rotational symmetry whose smallest angle is $45^\circ$. Such a figure would have rotational symmetry of order 8.
An example of such a figure is a regular octagon.
Answer: Yes.
b. Can we have a figure with rotational symmetry whose smallest angle of symmetry is 17°?
To check this, we see if $360^\circ$ is divisible by $17^\circ$.
$\frac{360^\circ}{17^\circ} = \frac{360}{17} $
We perform the division:
$360 \div 17$
17 goes into 36 twice with a remainder of $36 - (17 \times 2) = 36 - 34 = 2$. Bring down the 0 to get 20. 17 goes into 20 once with a remainder of $20 - (17 \times 1) = 3$. The division does not result in an integer.
The result is approximately 21.176.
Since $360/17$ is not an integer, $17^\circ$ is not a divisor of $360^\circ$.
This means it is not possible for $17^\circ$ to be the smallest angle of rotational symmetry for any figure, because a rotation by $360^\circ$ would not be an integer multiple of $17^\circ$, contradicting the property that $360^\circ$ must be an angle of symmetry.
Answer: No.
Question 7. This is a picture of the new Parliament Building in Delhi.

a. Does the outer boundary of the picture have reflection symmetry? If so, draw the lines of symmetries. How many are they?
b. Does it have rotational symmetry around its centre? If so, find the angles of rotational symmetry.
Answer:
We are analyzing the symmetry of the outer boundary shape of the New Parliament Building as shown in the picture.
a. Does the outer boundary of the picture have reflection symmetry? If so, draw the lines of symmetries. How many are they?
By observing the outer boundary shape, which resembles a hexagon with three prominent extensions, we can identify lines that divide the shape into two mirror images.
Yes, the outer boundary of the picture appears to have reflection symmetry.
There are lines of symmetry that pass through the center of the figure and extend outwards, dividing the shape symmetrically.
Due to the presence of three identical projecting sections, there are likely three lines of symmetry.
Description of lines of symmetry: These lines pass through the center of the figure and bisect each of the three projecting sections, extending radially outwards.
There are 3 lines of reflection symmetry.
b. Does it have rotational symmetry around its centre? If so, find the angles of rotational symmetry.
By observing the outer boundary shape, we can see if it can be rotated about its center to coincide with its original position.
Yes, the outer boundary has rotational symmetry around its center.
Since there are three identical projecting sections equally spaced around the center, rotating the figure by $360^\circ / 3 = 120^\circ$ will make it look exactly the same.
The smallest angle of rotational symmetry is $120^\circ$. The other angles of symmetry are integer multiples of the smallest angle, up to $360^\circ$.
The angles of rotational symmetry are: $1 \times 120^\circ = 120^\circ$, $2 \times 120^\circ = 240^\circ$, and $3 \times 120^\circ = 360^\circ$.
The angles of rotational symmetry are $120^\circ$, $240^\circ$, and $360^\circ$.
Question 8. How many lines of symmetry do the shapes in the first shape sequence in Chapter 1, Table 3, the Regular Polygons, have? What number sequence do you get?
Answer:
Referring to the first shape sequence in Chapter 1, Table 3, which lists the Regular Polygons, the shapes are typically listed in increasing order of the number of sides.
The shapes are:
- Equilateral Triangle (3 sides)
- Square (Regular Quadrilateral, 4 sides)
- Regular Pentagon (5 sides)
- Regular Hexagon (6 sides)
- Regular Heptagon (7 sides)
- Regular Octagon (8 sides)
- ... and so on.
The number of lines of symmetry for a regular polygon is equal to the number of sides it has.
- An Equilateral Triangle (3 sides) has 3 lines of symmetry.
- A Square (4 sides) has 4 lines of symmetry.
- A Regular Pentagon (5 sides) has 5 lines of symmetry.
- A Regular Hexagon (6 sides) has 6 lines of symmetry.
- A Regular Heptagon (7 sides) has 7 lines of symmetry.
- A Regular Octagon (8 sides) has 8 lines of symmetry.
- ... and so on for regular polygons with more sides.
The number sequence we get from the number of lines of symmetry of these regular polygons is the sequence of positive integers starting from 3.
The number sequence is: 3, 4, 5, 6, 7, 8, ...
Question 9. How many angles of symmetry do the shapes in the first shape sequence in Chapter 1, Table 3, the Regular Polygons, have? What number sequence do you get?
Answer:
Referring to the first shape sequence in Chapter 1, Table 3, which lists the Regular Polygons, the shapes are the Equilateral Triangle, Square, Regular Pentagon, Regular Hexagon, etc.
For a regular polygon with $n$ sides, the order of rotational symmetry is $n$. The number of angles of rotational symmetry (including $360^\circ$) is equal to the order of rotational symmetry.
So, a regular polygon with $n$ sides has $n$ angles of rotational symmetry.
- An Equilateral Triangle (3 sides) has 3 angles of symmetry ($120^\circ, 240^\circ, 360^\circ$).
- A Square (4 sides) has 4 angles of symmetry ($90^\circ, 180^\circ, 270^\circ, 360^\circ$).
- A Regular Pentagon (5 sides) has 5 angles of symmetry ($72^\circ, 144^\circ, 216^\circ, 288^\circ, 360^\circ$).
- A Regular Hexagon (6 sides) has 6 angles of symmetry ($60^\circ, 120^\circ, 180^\circ, 240^\circ, 300^\circ, 360^\circ$).
- A Regular Heptagon (7 sides) has 7 angles of symmetry ($360/7^\circ, 2 \times 360/7^\circ, \dots, 360^\circ$).
- A Regular Octagon (8 sides) has 8 angles of symmetry ($45^\circ, 90^\circ, 135^\circ, 180^\circ, 225^\circ, 270^\circ, 315^\circ, 360^\circ$).
- ... and so on for regular polygons with more sides.
The number sequence we get from the number of angles of symmetry of these regular polygons is the sequence of positive integers starting from 3.
The number sequence is: 3, 4, 5, 6, 7, 8, ...
Question 10. How many lines of symmetry do the shapes in the last shape sequence in Chapter 1, Table 3, the Koch Snowflake sequence, have? How many angles of symmetry?
Answer:
Referring to the last shape sequence in Chapter 1, Table 3, the Koch Snowflake sequence starts with an equilateral triangle and then adds smaller equilateral triangles to the middle third of each side in a recursive manner.
Number of lines of symmetry:
The starting shape of the Koch Snowflake is an equilateral triangle. An equilateral triangle has 3 lines of symmetry.
At each step of the construction, smaller equilateral triangles are added symmetrically to each side. Since the additions are done identically on all sides and maintain the initial symmetry of the equilateral triangle, the overall shape retains the same lines of symmetry as the initial equilateral triangle.
The lines of symmetry for the Koch Snowflake pass through each vertex of the initial equilateral triangle and the midpoint of the opposite side.
Therefore, the Koch Snowflake has 3 lines of symmetry at every stage of its construction.
Number of angles of symmetry:
The starting shape, the equilateral triangle, has rotational symmetry of order 3. Its angles of symmetry are $120^\circ$, $240^\circ$, and $360^\circ$. It has 3 angles of symmetry (including $360^\circ$).
Since the construction adds identical fractal details symmetrically to each side in a way that respects the $120^\circ$ rotation, the rotational symmetry is also preserved at each step.
Rotating the Koch Snowflake by $120^\circ$ about its center makes it coincide with its original position.
Therefore, the Koch Snowflake has rotational symmetry of order 3.
The angles of rotational symmetry are the same as those of the initial equilateral triangle: $120^\circ$, $240^\circ$, and $360^\circ$.
The Koch Snowflake has 3 angles of symmetry.

Answer:
The Ashoka Chakra, as depicted in the center of the Indian flag, is a wheel with 24 equally spaced spokes.
Number of lines of symmetry:
A figure with $n$ equally spaced elements arranged around a center typically has $n$ lines of symmetry. In the Ashoka Chakra, there are 24 equally spaced spokes radiating from the center.
Each line passing through the center and one of the spokes is a line of symmetry.
Each line passing through the center and lying exactly between two adjacent spokes is also a line of symmetry.
Since there are 24 spokes, there are 24 lines of symmetry.
The Ashoka Chakra has 24 lines of symmetry.
Number of angles of symmetry:
A figure with $n$ equally spaced elements arranged around a center has rotational symmetry of order $n$. The number of angles of rotational symmetry (including $360^\circ$) is equal to the order of rotational symmetry, which is $n$.
The Ashoka Chakra has 24 equally spaced spokes, so it has rotational symmetry of order 24.
The smallest angle of rotational symmetry is $360^\circ / 24 = 15^\circ$.
The angles of rotational symmetry are the multiples of $15^\circ$ up to $360^\circ$: $15^\circ, 30^\circ, 45^\circ, \dots, 360^\circ$. There are 24 such angles.
The Ashoka Chakra has 24 angles of symmetry.

